I love bringing ideas to life through designs and simulations. Design to me is the cross-section of engineering and the arts, and simulation the bridge between the virtual world of design and the real-world.
Design Portfolio
You can rotate, ZOOM In and expande the 3d designs
Spare a few seconds for the designs to load
Rotor
Mechanical ENGINEERING
Course
Basic Engineering Graphics and Computer Aided Design (ENGR 1020)
Overview
A rotor is the moving component of an electromagnetic system that receives electical energy produced from a stator's magnetic field and then transmits mechanical power through the system.
Designed with
SolidWorks
Parts
1. Shaft
2. Core plates
3. Coil windings
4. Metal Contacts
5. Contact holders
DC Motor
ELECTROMECHANICAL Engineering
Course
Basic Engineering Graphics and Computer Aided Design (ENGR 1020)
Overview
A DC motor is an electrical device that converts electrical energy from a DC source to mechanical energy through electromagnetic principles.
Designed with
SolidWorks
Parts
1. Motor housing
2. End contact
3. Magnet
4. Spacer
5. Bushings
6. Rear cover
7. Spur gear
Servo Motor
ELECTROMECHANICAL Engineering
Course
Basic Engineering Graphics and Computer Aided Design (ENGR 1020)
Overview
This servo motor is a rotary actuator that enables the precise control of angular position, velocity and acceleration.
Designed with
SolidWorks
Parts
1. Servo motor housing
2. DC Motor
3. Integrated Circuit
4. Position Potentiometer
5. Multiple gears
Interbotix X-Series Robotic Arm
Robotics
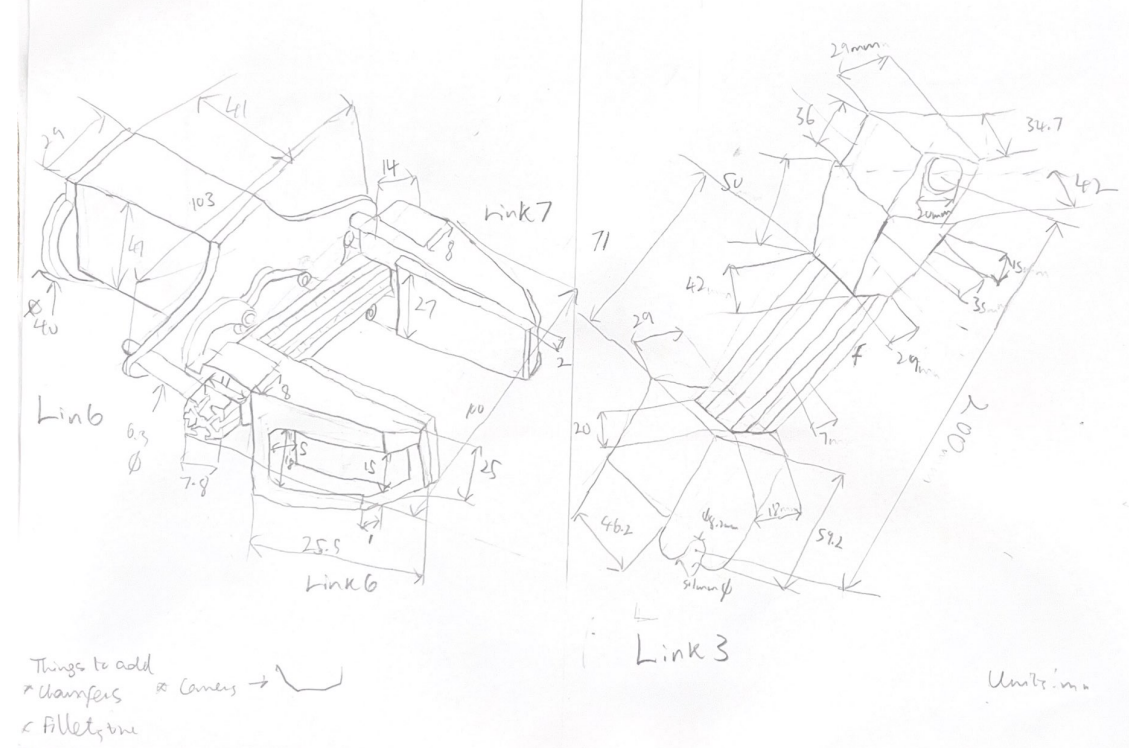
Hand Sketches of Link 3 and Link 6
Designed with
Solidworks
Course
Robotics (MENG 4900)
Overview
This designed was made by from hand-made measurements of the Interbotix X-series arm which was translated into a CAD model. This was part of a larger project, developing a Robotics 3D Visualisation and Control Application.
Performed
1. Manual measurements
2. Hand-made sketches
3. SolidWorks design
Air Hockey Score Board
eLECTRONICS Design & manufacturing
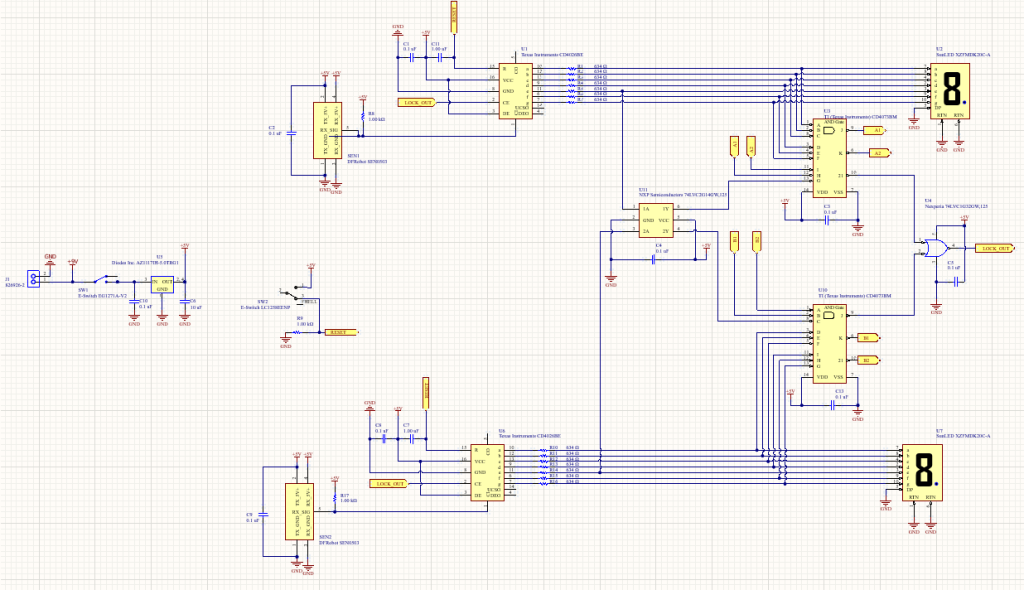
Schematic View
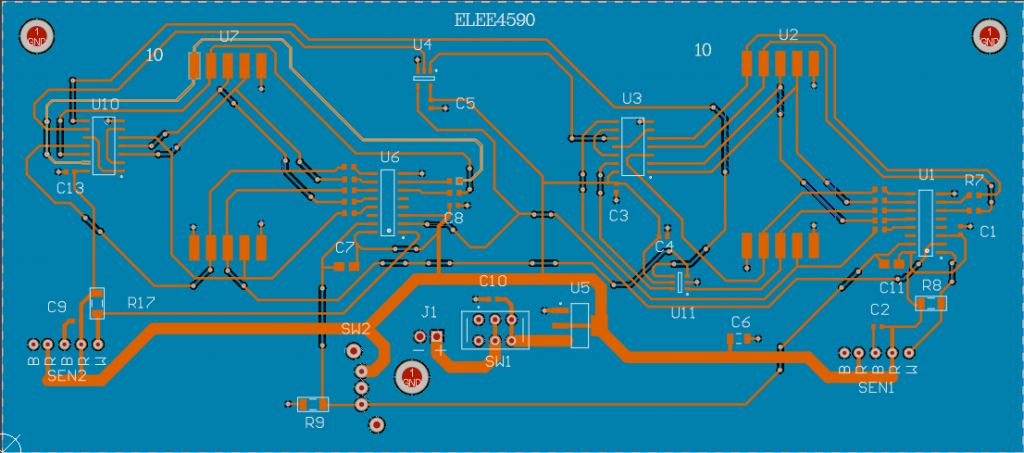
Front 2D View

Front 3D View

Rear 3D View

Front Reality View

Rear Reality View
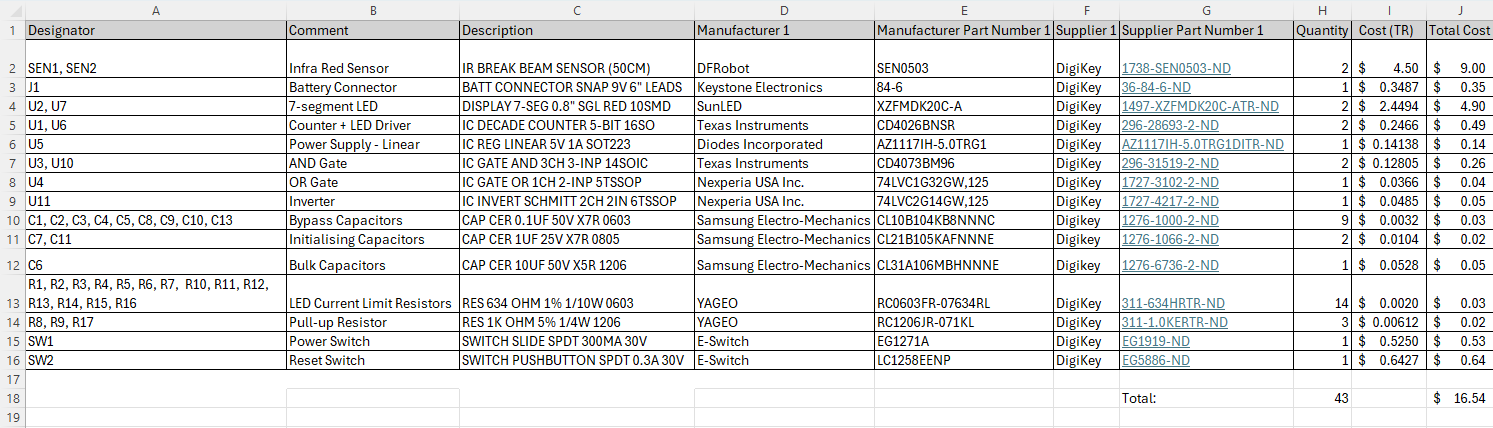
Bill of Materials
Course
Electronics Manufacturing (ELEE 4590)
Overview
Designed a cost-effective Air Hockey Score Board using the knowledge of Digital logics, Electrical Circuit design and Electronics development. With a projected total production cost of $23.15, the board is cheaper than the baseline design by 40.38%.
Designed with
Altium CircuitMaker
Fusion Thermal Cup
product development

Course
Computer Aided Engineering (ENGR 4920)
Overview
The Fusion thermal cup was inspired by Nigerian and Chinese Culture and is presented as a product called the Delang thermal cup (a combination of letters from our state and province of origin). It meant for use for storing liquids and to be accessible by persons with hand/arm-related disabilities. The cup has good thermal insulation as Calabash is a good insulator. It takes about It takes about 52 minutes (very close to an hour) for the average temperature of water to drop by 30 degrees Fahrenheit from 130 degrees Fahrenheit. This was determined through SolidWorks Thermal Simulation.
Designed with
SolidWorks
Parts & Design
1. Double wall made of Calabash (native to Nigeria)
2. Main body based on Chinese cups and the lid of Nigerian Calabash lids
3. Internal Layer that contacts with liquid, made off AISI 304, a stainless steel alloy
4. Finger mechanism for single hand opening of the thermal cup (Ease of use for persons with hand/arm-related disabilities
74LS93 Counter Integrated Circuit (IC)
eLECTRONICS: Digital logics
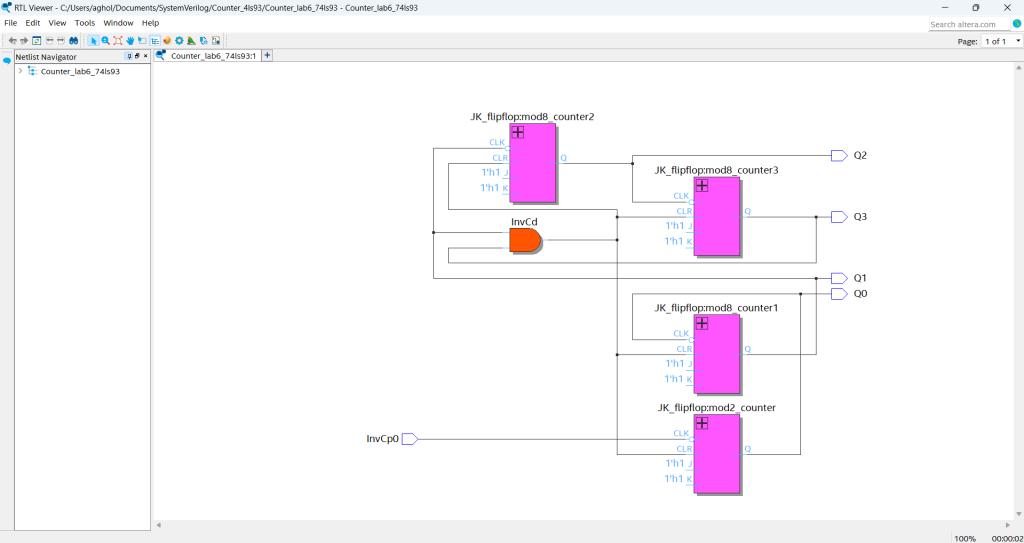
Unexpanded form
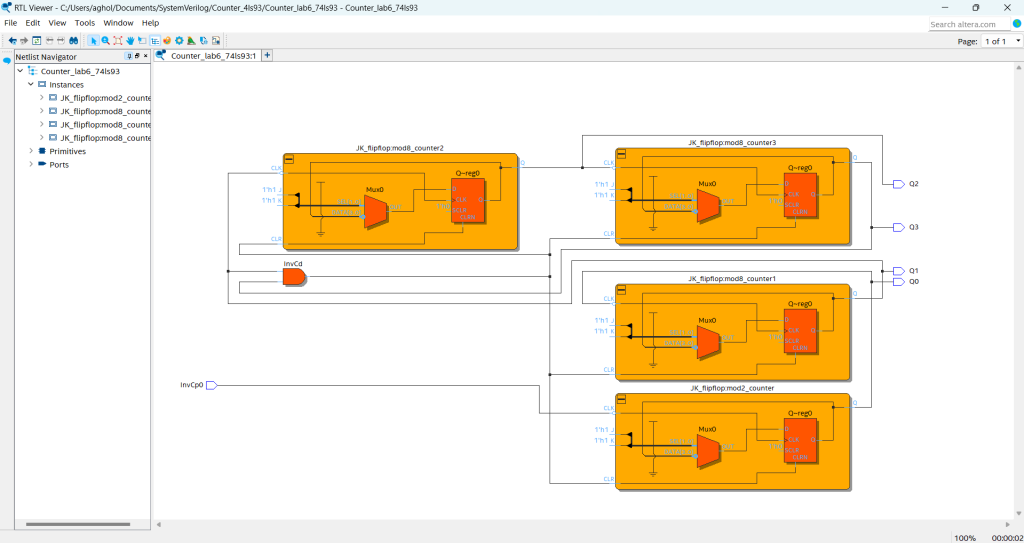
Expanded form
Course
Digital Logics & its Lab (ELEE 2640 & 2650
Overview
Counters such as 74ls93 are sequential circuits which can be designed with JK flip-flops and simulated using the Quartus application. These sequential circuits go through a defined sequence of states upon the application of input impulses.
Designed with
1. System Verilog
2. VHDL
3. Quartus Prime
Performed
1. Recreated the counter using System Verliog and VHDL on the Quartus prime software.
2. A JK flipflop was developed and then used as a module incorporated 4 times to produce the counter and achieve its functionality.
3. Performed a simulation testing the Counter IC design, achieving the same results as specified by the manufacturer truth table.
Field-controlled DC motor
Controls engineering
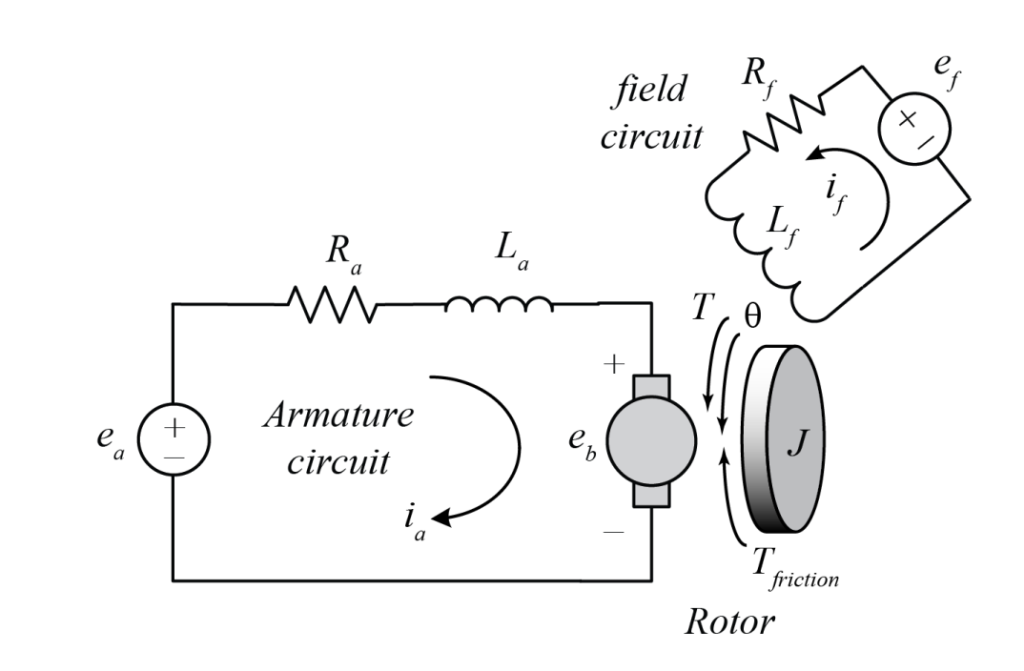
Motor Schematic
Provided by Professor Richard Hill
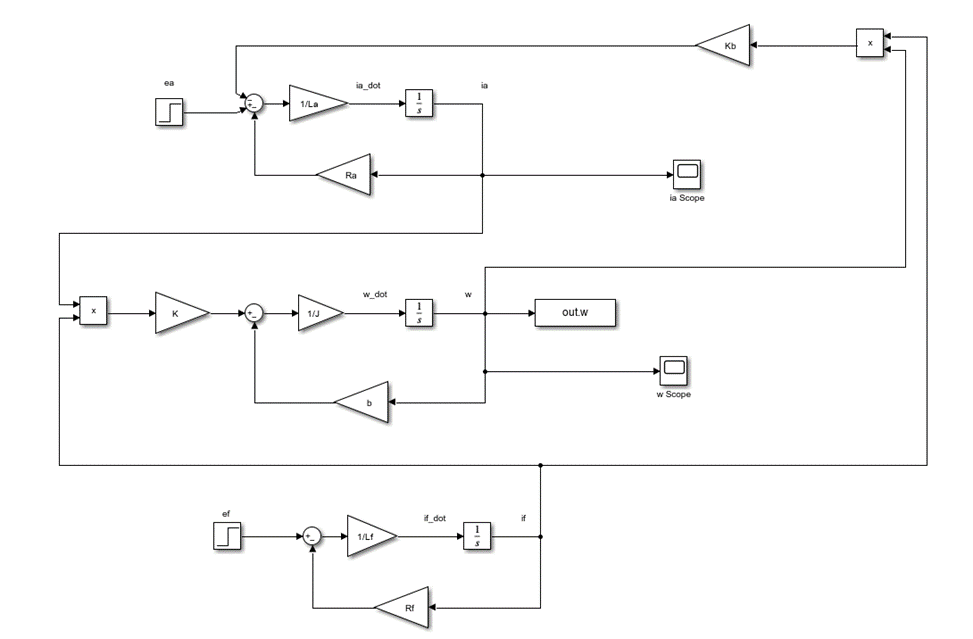
Simulink Model Design
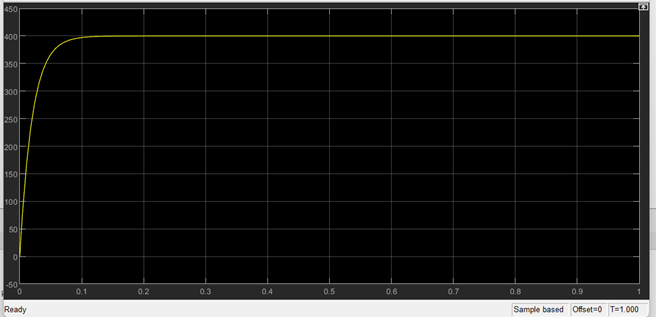
ARMATURE CURRENT OUTPUT ia RESPONSE
It approaches 400 A
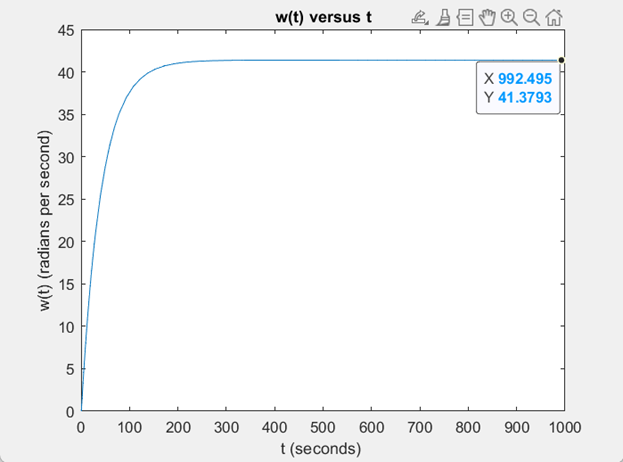
MOTOR SPEED RESPONSE w(t)
The motor speed approaches 41.3793 radians per second
Course
Control Systems (ENGR 4220)
Developed with
1. Simulink
2. MATLAB
Overview
The field-controlled DC motor has a constant armature voltage (ea) constant, and its speed the speed is controlled by varying the strength of the magnetic field. This is controlled by the field voltage (ef) . The armature circuit has a back emf due to the rotation of the armature. However, the field circuit is stationary; so it has no back emf.
Performed
1. Derived a non-linear differential equation model from the schematic
2. Used Simulink to create a model and simulation
3. Loaded values of constants in the model from a MATLAB script
4. With Matlab some of the simulation results were formatted
Constant Parameters
1. Rf = 240 Ω
2. b = 0.02 Nm/rad/s
3. Lf = 120 H
4. K = 0.0025 Nm/A^2
5. J = 1 kg-m^2
6. La = 0.012 H
7. Ra = 0.6 Ω
8. Kb = 1 V-s/rad
Simplified Automobile Model
Controls engineering
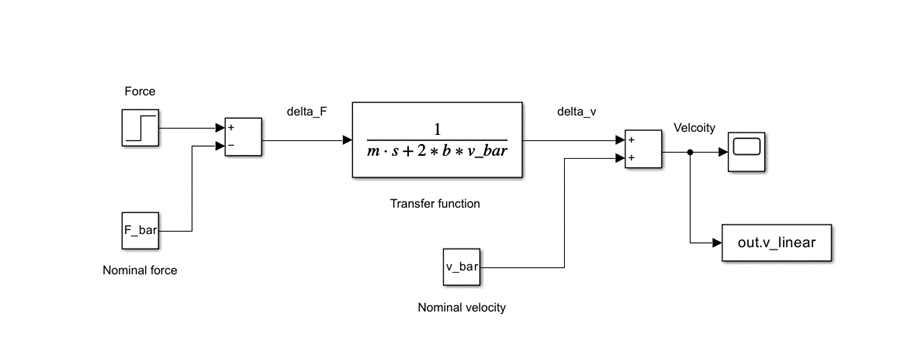
Linear Transfer Function Model
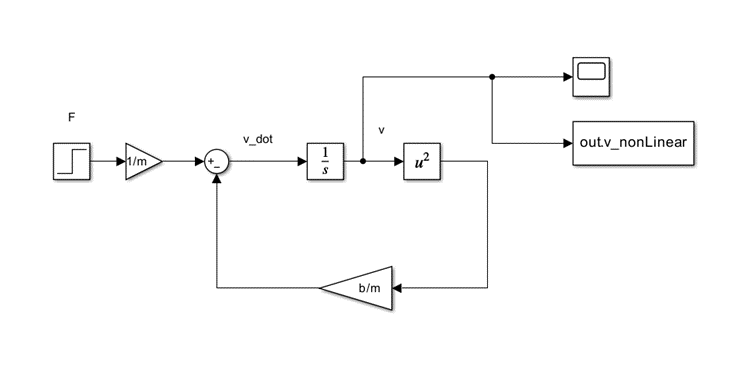
Nonlinear Model
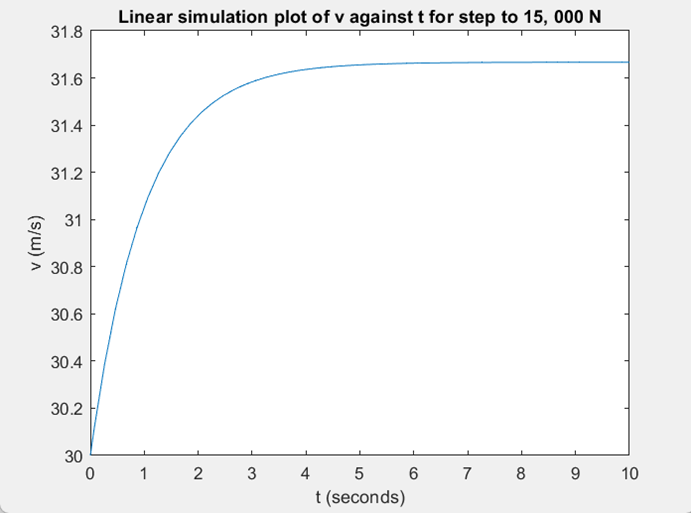
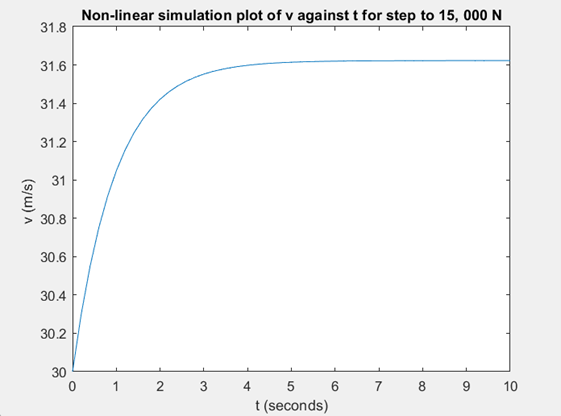
Both approach 31.6 m/s
Course
Control Systems (ENGR 4220)
Designed with
1. Simulink
2. MATLAB
Overview
An automobile can be very simplified by a model that only has the interaction between two forces upon the body of the car., the force that propels the car forward and drag.
Constant Parameters
1. m = 900 kg
2. b = 15 kg/m
3. F¯ = 13, 500 N
4. v¯ = 30 m/s
Performed
1. Designed a a non-linear differential equation model from the differential equation model
2. Produced a linear transfuction model from the linearised version of the differential equation
3. Used Matlab to format the simulation results
4. Loaded values of constants in the model from a MATLAB script
